Introduction
Recently, I just finished CS50 Week3, and the topic of this week is: Algorithms. It introduces several classic sorting algorithms, such as selection sort, bubble sort, insertion sort, and merge sort.
As a software engineer, I think we can never escape from sorting algorithms. After all, this is one of the classic algorithms! Instead of preparing for interviews in a mess every time, it’s better to organize a post now to record the experience of each sorting algorithm and help ourselves to integrate.
Therefore, this post will use JavaScript to implement various classic sorting algorithms.
The sorting algorithms implemented this time will be sorted from small to large, and for convenience, each sorting algorithm “will directly modify the original array”. But if you don’t want to modify the original, it’s easy. Just add arr = arr.slice() at the beginning of each function to copy the original.
Also, because it is difficult to put animations in the article, I can only put some pictures. If you want to learn with visualized algorithms, I highly recommend VISUALGO. This website will definitely take your understanding of sorting to the next level.
Selection Sort
I think selection sort is the easiest sorting algorithm to understand because its principle is super simple:
Find the minimum value and move it to the leftmost.
After you finish the first round, you will find the minimum value of the entire array, and then you change the search range from 0 ~ n-1 to 1 ~ n-1 and repeat the same thing. Or, you can also think of it as: find the minimum value, the second smallest value, the third smallest value… the n-th smallest value.

(Image source: http://cheetahonfire.blogspot.sg/2009/05/selection-sort-vs-insertion-sort.html)
const selectionSort = (arr) => {
const length = arr.length;
// Find the minimum value for how many elements there are
// Here, i represents that all elements before i are sorted
for (let i = 0; i < length; i++) {
// First assume that the first one is the smallest
let min = arr[i];
let minIndex = i;
// Find the minimum value from the unsorted elements
for (let j = i; j < length; j++) {
if (arr[j] < min) {
min = arr[j];
minIndex = j;
}
}
// ES6 syntax, swap two values
[arr[minIndex], arr[i]] = [arr[i], arr[minIndex]];
}
return arr;
}The time complexity is the well-known O(n^2), and the best, worst, and average are all the same, because no matter how long the original array is, it has to go through so many rounds of comparison.
Bubble Sort
Bubble sort should be the first sorting algorithm that many people come into contact with, and the principle is also very simple and easy to understand:
Compare with the neighbor, exchange the order if it is wrong, and let the larger elements keep moving to the end.
It is the process of exchanging like this that makes it called “bubble” sort, because the elements are like “floating” up.
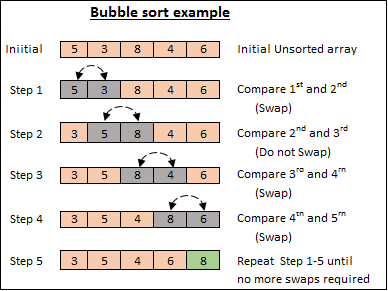
(Image source: http://www.opentechguides.com/how-to/article/c/51/bubble-sort-c.html)
const bubbleSort = (arr) => {
const n = arr.length;
// A total of n rounds need to be run
for (let i = 0; i < n; i++) {
// Start from the first element and keep running to the n - 1 - i element
// Originally it was n - 1, and - i was added because the last i elements have been sorted
// So there is no need to compare with those sorted elements
for (let j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}Although the average and worst-case time complexity of Bubble Sort is O(n^2), it is worth noting that the best case occurs when the input array is already sorted. In this case, the time complexity is O(n), and no exchanges are made.
However, if you want to achieve the best case of O(n), you must add a small optimization. Otherwise, in the case mentioned above, although no exchanges are made, every element is still checked.
You can add a flag to indicate whether there is any exchange in the inner loop. If not, it means that the array is already sorted, and you can skip it directly.
function optimzedBubbleSort = (arr) => {
const n = arr.length;
let swapped = true;
// A total of n rounds are required
for (let i = 0; i < n && swapped; i++) {
// Start from the first element and keep running to the n - 1 - i th element
// Originally n - 1, adding - i because the last i elements are already sorted
// So there is no need to compare with those sorted elements
swapped = false;
for (let j = 0; j < n - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swapped = true;
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}After the improvement, if the input is already sorted, the inner loop will only run once and then skip, so the time complexity will be O(n).
Insertion Sort
Insertion Sort is a sorting algorithm that I think is quite intuitive. In short:
The sorting algorithm you use when playing poker
It’s just constantly inserting cards into the appropriate position, but when you play cards, you may insert many cards at once, while Insertion Sort inserts one card at a time.
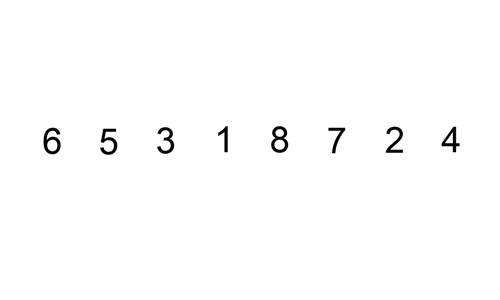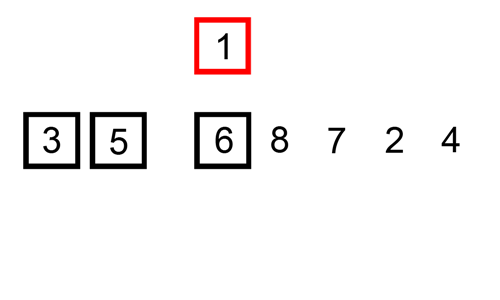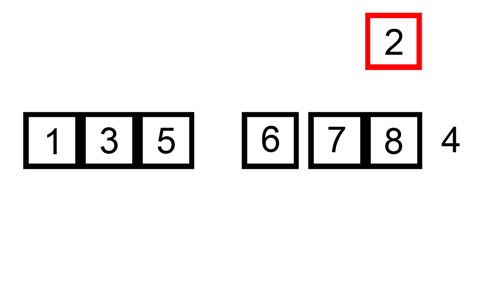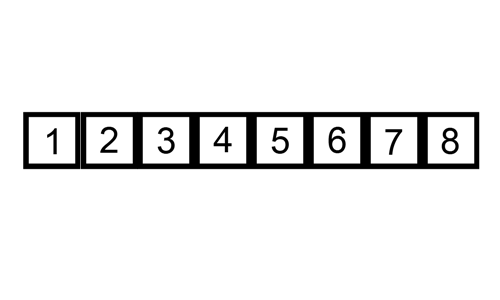
(Image source: https://commons.wikimedia.org/wiki/File:Insertion-sort-example.gif)
What is worth noting here is the algorithm for insertion. Continuously find the appropriate position and move the elements while finding, so you can insert directly when you find it.
const insertionSort = (arr) => {
const n = arr.length;
// Assuming that the first element is already sorted, start from 1
for (let i = 1; i < n; i++) {
// position indicates the position where it can be inserted
let position = i;
// First save the element to be inserted
const value = arr[i];
// Start looking forward, as long as this condition is met, it means that this position can be inserted
// You can move the element backward while looking for it to make room
while (i >= 0 && arr[position - 1] > value) {
[arr[position], arr[position - 1]] = [arr[position - 1], arr[position]];
position--;
}
// Find the appropriate position and insert the element
arr[position] = value;
}
return arr;
}The best case of Insertion Sort occurs when the input elements are already sorted. In this case, the while loop inside only runs once, so the time complexity is only the outer loop’s O(n).
Here’s a little anecdote. When I was writing the demonstration and testing code, I didn’t write it well, so the arrays used for testing were already sorted. I thought, “Why is Insertion Sort faster than Quick Sort? It doesn’t make sense!”
Merge Sort
Next, we will move on to a faster sorting algorithm, Merge Sort, which is relatively easy to understand:
Cut in half, sort the left and right sides, and merge them.
When talking about Merge Sort, I like to talk about the merge step first, which is to merge two separately sorted arrays into one. This step is actually quite simple because both sides are already sorted, so just keep looking at the first element of both sides and grab the smaller one. Then, grab the remaining elements from the left or right side.
I previously found a version of merge sort that is easier to understand but consumes more space:
const simpleMergeSort = (arr) => {
// Merge
const merge = (leftArray, rightArray) => {
let result = [];
let nowIndex = 0, left = 0, right = 0;
const leftLength = leftArray.length;
const rightLength = rightArray.length;
// If both left and right sides are not empty, compare and add the smaller one to the result array
while (left < leftLength && right < rightLength) {
if (leftArray[left] < rightArray[right]) {
result[nowIndex++] = leftArray[left++];
} else {
result[nowIndex++] = rightArray[right++];
}
}
// If one side is empty, add the remaining elements from the other side to the result array
while (left < leftLength) {
result[nowIndex++] = leftArray[left++];
}
while (right < rightLength) {
result[nowIndex++] = rightArray[right++];
}
// Return the merged array
return result;
}
const _mergeSort = (arr) => {
const length = arr.length;
if (length <= 1) return arr;
// Divide the array into two halves
const middle = Math.floor(length / 2);
// Sort the left half
const leftArray = _mergeSort(arr.slice(0, middle));
// Sort the right half
const rightArray = _mergeSort(arr.slice(middle, length));
// Merge the two halves and return the result
return merge(leftArray, rightArray);
}
return _mergeSort(arr);
}For me, the simpler version is more intuitive because you just slice the array into two halves, sort them, and then merge them back together.
However, the more space-efficient approach is to modify the original array directly. In this case, the parameters are a bit different:
function mergeSort = (arr) => {
const merge = (array, start, middle, end) => {
// Declare a temporary array to hold the merged result
let temp = [];
let nowIndex = 0;
let left = start;
let right = middle + 1;
// Same as before
while (left <= middle && right <= end) {
if (array[left] < array[right]) {
temp[nowIndex++] = array[left++];
} else {
temp[nowIndex++] = array[right++];
}
}
while (left <= middle) {
temp[nowIndex++] = array[left++];
}
while (right <= end) {
temp[nowIndex++] = array[right++];
}
// Put the merged array back into array[start ~ end]
for (let i = start; i <= end; i++) {
array[i] = temp[i - start];
}
}
// Sort from start to end
const _mergeSort = (array, start, end) => {
if (end <= start) return;
const middle = Math.floor((start + end) / 2);
// Sort the left and right halves
_mergeSort(array, start, middle);
_mergeSort(array, middle + 1, end);
merge(array, start, middle, end);
return array;
}
return _mergeSort(arr, 0, arr.length - 1);
}Because it directly modifies the original array, you need to pass in a few more numbers to indicate which part of the array you want to sort. After calling the function, you can assume that the specified part of the array is already sorted.
The basic process is the same as the simplified version above, but it saves some memory space.
Quick Sort
At first, I thought Quick Sort was quite complicated, but after understanding the principle, I found it not that difficult. The principle is actually quite simple:
Find a number and adjust it so that the elements on the left are smaller than it, and the elements on the right are larger than it. Then do the same thing on both sides.
We call that number the pivot, which divides the sequence into two sides.
For example, if we have a sequence: 14, 7, 6, 9, 10, 20, 15
We choose 14 as the pivot, and after adjustment, it becomes: 7, 6, 9, 10, 14, 20, 15. All the elements on the left are smaller than it, and all the elements on the right are larger than it.
When you adjust 14, this element is actually sorted! Because the left is smaller than it, and the right is larger than it, so this number is sorted. Then just do Quick Sort on the two sides that have not been sorted yet.
The core of Quick Sort is how to find that number. If you find the median of the sequence, the efficiency is the highest. If you find the smallest number, it is the worst case, and the time complexity becomes O(n^2), which is the same as not dividing.
We assume that the first number is the pivot, which is more convenient.
Another problem is how to adjust the number to make the left smaller than it and the right larger than it. We can maintain a variable called splitIndex, so that all the elements to the left of this index are smaller than the pivot, and this index itself and the elements to the right of it are larger than the pivot.
When you scan the array and find an element smaller than the pivot, swap this element with the element at splitIndex, and then increase splitIndex by 1. Finally, remember to swap the pivot with the last element smaller than it, which can put the pivot in the correct position.
You can refer to the gif below or go to VISUALGO to see it.
(Source: https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/6.quickSort.md)
function quickSort = (arr) => {
const swap = (array, i , j) => {
[array[i], array[j]] = [array[j], array[i]];
}
const partition = (array, start, end) => {
let splitIndex = start + 1;
for (let i = start + 1; i <= end; i++) {
if (array[i] < array[start]) {
swap(array, i, splitIndex);
splitIndex++;
}
}
// Remember to swap the pivot with the last element smaller than it
swap(array, start, splitIndex - 1);
return splitIndex - 1;
}
const _quickSort = (array, start, end) => {
if (start >= end) return array;
// Adjust the sequence in partition and return the index of the pivot
const middle = partition(array, start, end);
_quickSort(array, start, middle - 1);
_quickSort(array, middle + 1, end);
return array;
};
return _quickSort(arr, 0, arr.length - 1);
}Heap Sort
Heap is a data structure, and there are two types: max heap and min heap. The principles of the two types are actually the same, and we will talk about max heap directly.
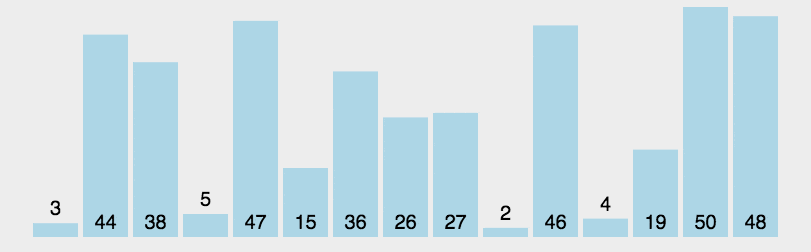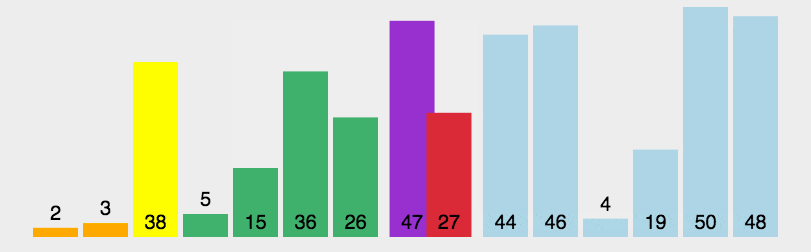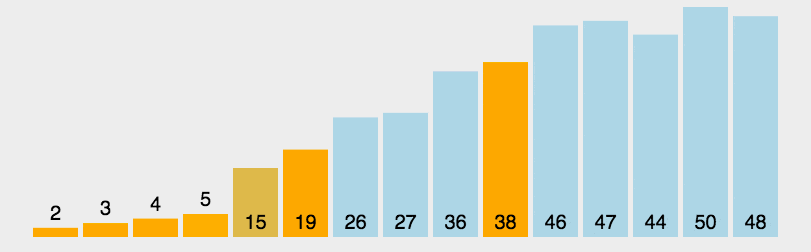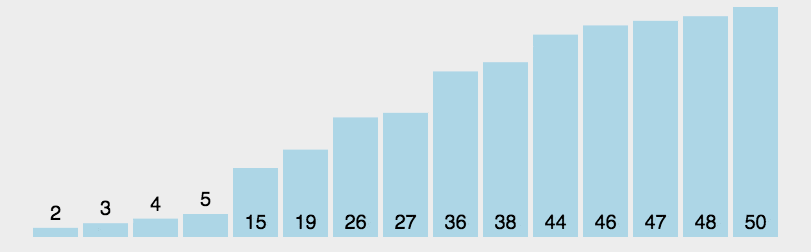
Let’s take a look at a picture of max heap:
(Source: https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm)
You can see that the max heap satisfies two properties:
- The parent node is always greater than the child node.
- The root node of the entire tree is always the maximum value (which can be deduced from 1).
It is also easy to represent the heap using an array, like this:
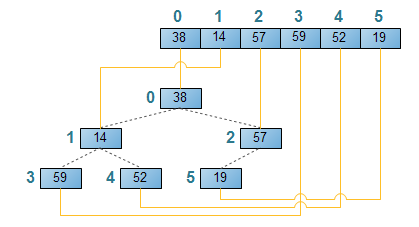
(Source: http://notepad.yehyeh.net/Content/Algorithm/Sort/Heap/Heap.php)
So heap sort uses this data structure for sorting, and the process is simple:
- First, build the max heap of the array read in (at this time, arr[0] is definitely the maximum value of this array).
- Swap arr[0] with the last node (which is actually the last unsorted node).
- Adjust to max heap and return to step 2.
Heap sort is actually a bit complicated, complicated enough to be a separate article…
But in simple terms, it is an improved version of selection sort, selecting the maximum value each time, and then adjusting the remaining numbers to max heap.
function heapSort = (arr) => {
function heapify(arr, length, node) {
const left = node * 2 + 1;
const right = node * 2 + 2;
// Assume that the largest node is itself first
let max = node;
if (left < length && arr[left] > arr[max]) {
max = left;
}
if (right < length && arr[right] > arr[max]) {
max = right;
}
// If either the left or right side is larger than the node
if (max !== node) {
// Swap the two
[arr[node], arr[max]] = [arr[max], arr[node]];
// Then continue to heapify
heapify(arr, length, max);
}
}
// build max heap
const length = arr.length;
for (let i = Math.floor(length / 2) - 1; i>=0; i--) {
heapify(arr, length, i);
}
// Sort
for (let i = length - 1; i > 0; i--) {
[arr[0], arr[i]] = [arr[i], arr[0]];
heapify(arr, i, 0);
}
return arr;
}Summary
After careful study, you will find that every sorting algorithm has something worth referencing, and each sorting method is quite interesting. You will also find that understanding the principles is one thing, and whether or not you can write it is another. This article can be regarded as my own sorting algorithm notes. If there are any errors, please let me know.
If you want to try it out for yourself, I have put it on Github (https://github.com/aszx87410/JavaScript-sorting-algorithm-demo), with test cases already written. You can modify it and test it directly, which should be quite convenient.
Because of the testing process, each sorting algorithm is prefixed with: arr = arr.slice() to avoid modifying the original array.
The testing process is also quite interesting. I found that some ES6 syntax (such as the trendy swap syntax or even let) sometimes slows down execution speed. Therefore, I previously changed all the syntax back to ES5 and found that the efficiency was much faster, but this article is not about efficiency, so all the syntax is still in ES6.
Comments